2=1

As many people, we came across the following photo:

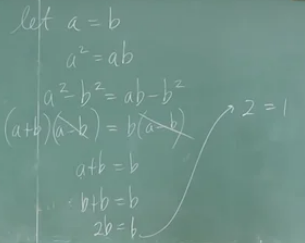
In this mathematical “proof” the author tries to convince us that there is an error in math and it can be demonstrated using the above example. The steps taken by this person are the following:

1. The proof starts by defining a equal to b (a = b).
2. Then, it multiplies both sides with a which results to a^2 = ab.
3. Next, it subtracts from both sides b^2 and we get a^2-b^2 = ab-b^2.
4. Following, it extracts the common multiplier of both sides (a-b) resulting to (a+b)(a-b) = b(a-b).
5. Here’s the nice part, the author divides both sides with (a-b) which results to a+b = b.
6. Since a = b, it replaces a on the left side with a b and produces this state b+b = b => 2b = b.
7. Finally, it divides by b both sides which results to 2 = 1.

The reason that this proof is false is because in step 5, where it divides both sides with (a-b) it really is dividing both sides with 0 (since we know for sure that a = b from step 1) which it cannot be defined as a valid division. So everything from step 5 and forward are invalid and thus the proof is wrong.